Many business situations are subject to significant uncertainty. What are the chances of one or more serious accidents in our worldwide operations in a given period? Or two or more key business process interruptions over the same time? Or three or more sales from 16 appointments? Or two heads in two flips of a fair coin?
Understanding these probabilities, and how to manage or improve them, could be life-saving. Misunderstanding, or applying the wrong model, could court disaster.
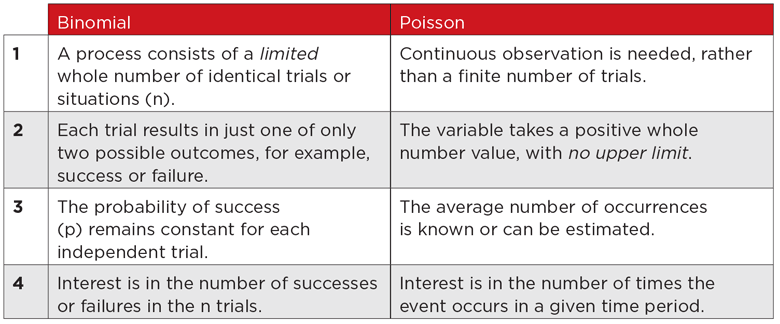
Some uncertain situations can be analysed using a simple probability model. For example, the coin flip. Practical business situations are usually much more complex, but probability models can still be useful tools to start our analysis. Recently examined models include the binomial and Poisson distributions. We need to understand them both. But we also need to know when to use each of them, or neither of them, and how we can change the odds in our favour.
The ‘binomial’ part of the binomial distribution means it is built up from a number of ‘success’ or ‘fail’ trials. It is a good model for a limited series of simple, independent trials, such as coin flips. Let’s consider two flips of a fair coin and the probability of scoring two heads, a head being defined as a success. There is a limited number of independent trials, two, and a constant probability of success (p) in each trial, 0.5. The probability of failure, a tail in this case, is 1 – p. This is also 0.5 for a fair coin flip.
The probability of two heads from two flips modelled by the binomial is: 0.5 x 0.5 = 0.25, or 25%.
Similarly, the probability of three heads in three flips would be:
0.5 x 0.5 x 0.5 = 0.125, or 12.5%.
A key feature of binomial models is that the number of binomial trials is limited, and the maximum number of successes is also limited, namely to the total number of trials.
Most business risks aren’t as simple as that. Key business process interruptions or even serious accidents can happen at any time. Examples include apparently random interruptions, such as computers going down, phone calls or other types of faults.
These situations are better modelled by the Poisson distribution, rather than the binomial.
The time period is sometimes known as a ‘continuum’. This means:
Let’s take phone calls as an example. Say a phone rings, on average, twice per hour. If you leave your phone switched on when you’re studying, the total number of times it could ring, modelled by the Poisson distribution, is unlimited. And, on average, it is expected to ring twice per hour. Most unhelpful when our interest is in improving your probability (p) of passing your exam. That’s bad news, but we will see shortly that there is something very effective you can do to improve your chances.
In the meantime, let’s summarise and contrast both the binomial and Poisson models.
The table below would be an excellent answer to a recent exam question, which asked:
Economics & Statistical Analysis (ESA), April 2014, Q7(a)
Another part of the same question asked:
A car salesperson has 16 appointments with potential buyers. However, there is only a one-in-five chance that an appointment will result in a car being bought.
The salesperson will receive a bonus if at least three cars are bought as a result of the 16 appointments.
State whether the binomial or Poisson distribution is relevant in the given situation.
ESA, April 2014, Q7(b)
Is the binomial or the Poisson the better model here? Applying the characteristics we have identified, the number of sales appointments (trials) is limited, namely to the 16 appointments. For this reason, the number of successful appointments can never exceed 16. So the binomial distribution is relevant, and not the Poisson.
Candidates’ performance in this question was mixed. The examiner was particularly concerned by poor knowledge of the Poisson distribution.
The first requirement asked candidates to discuss the characteristics of both the binomial and Poisson distributions. Very few candidates scored highly in the Poisson discussion.
Examiner’s report, ESA, April 2014
Where did candidates go wrong? Probable causes could be:
If you don’t know something, or you’re not sure, set up a table and write down something relevant that you do know. This will help you to recall or guess at the parts you’re not so sure of.
For example, if you know about the binomial model, but aren’t sure about the Poisson, set up the table structure (see table below) and fill in the binomial parts to start with. Now it’s easier to remember or make sensible guesses for the Poisson, by comparing with the binomial.
Going back to the phone interruptions, here’s some great news: you don’t have to accept the initial modelling assumptions. You can shift the odds to be overwhelmingly in your favour. If you don’t want the phone to ring, simply switch it off or unplug it. Now it can’t ring.
Unplugging my phone was one of the most significant steps in my own exam successes. From then on, I was fully committed to my study.
You’ll undoubtedly switch off your phone for your real exam. If you don’t, the invigilator will ask you to leave. Otherwise it wouldn’t be fair to the other candidates. Be fair to yourself, and do the same when revising and practising past exam papers. Switch off distractions, focus in and prepare to step up to success.
Download previous articles from this series and other useful study information from the Exam tips area of the student site at study.treasurers.org/examtips
Doug Williamson FCT is a tutor, coach and former chief examiner. He understands study time is limited, but believes our potential to learn is unlimited
