
A normal distribution is an extremely useful (simplified) model for making predictions about real world distributions. The normal distribution is easy to use because it is:
The mean defines the midpoint of the normal distribution and the standard deviation defines how spread out it is.
A standard normal distribution is a (standardised) transformed version of any normal distribution. The standard normal distribution has a mean of 0 and a standard deviation of 1.
This is the version of the distribution that is set out in statistical tables like the one provided in your Economics and Statistical Analysis (ESA) exam, summarised below [See Note 1].
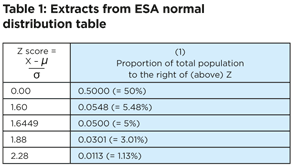
The ‘Z score’ in the table above is a number of standard deviations away from the mean. In this case, it is a number of standard deviations above the mean.
The proportions given in the table are the proportions of the total population, above the given Z score. For example, for a Z score of 1.6449 (1.6449 standard deviations above the mean), 5% of the total modelled population is above this point. This is the blue-shaded area in figure 1.
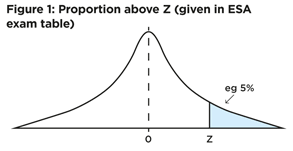
Looking at figures 2, 3 and 4, we can now work out the green, yellow and pink proportions as well (even though these aren’t expressly set out in the ESA table).
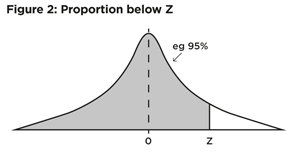
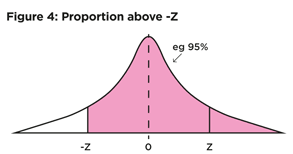
To do this, we use two of the important characteristics of the normal distribution: the total area under the curve is always 1 (100%); and the symmetry of the curve.
The other information we can work out is in table 2 below.
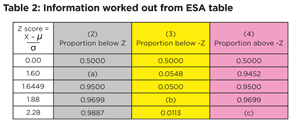
We calculate column (2), the green proportion below Z, as 1 (100%) less the proportion above Z (from table 1 above). The reason for this is that the total population, by definition, adds up to a total proportion of 1 (100%).
For example, for a Z score of 1.6449:
The blue proportion above Z from table 1 = 0.05 (5%).
So the green proportion below Z in table 2 column (2) above is calculated as 1 – 0.05 = 0.95 (95%).
This column is the green-shaded area in figure 2.
It’s your turn now. Please calculate the proportion below a Z score of 1.60, missing letter (a) in table 2. The answers are at the end of this article [See Note 2].
Column (3), the yellow proportion below -Z, is easier to work out. We use the symmetry around the midpoint of 0. The shape and proportions of the bottom half are the same as the top half, which we already know. From the symmetry around 0, the yellow proportion below -Z is the same as the blue proportion above +Z.
For example, for the same Z score of 1.6449:
The blue proportion above +Z from table 1 = 0.05 (5%).
So the yellow proportion below -Z in table 2 column (3), is also 0.05 (5%).
Your turn again. What is the proportion below a Z score of -1.88 (missing letter (b) in table 2)? [See Note 3]
The next section is slightly trickier.
Finally, we need the pink proportion above -Z (column (4)). We could calculate this as 1 less the proportion below -Z (from column (3)). The reason is that the total of the yellow area and the pink area is equal to 1.
For example, for the same Z score of 1.6449:
The yellow proportion below -Z = 0.05 (5%).
So the pink proportion above -Z = 1 – 0.05 = 0.95 (95%).
(From the symmetry of the distribution, this is also the same area as the green proportion below +Z in figure 2. So an alternative shorter calculation for the pink proportion above -Z in column (4) is simply 1 less the blue figure. For example, 1 – 0.05 = 0.95, as before.)
Please calculate the proportion above a Z score of -2.28, missing letter (c) in table 2. [See Note 4] This is the most important idea to get clear.
The final tool that we need for calculations in the ESA exam is the formula helpfully provided in the statistical table [See Note 5]:
Z score =
This formula converts raw data (X) into a number of standard deviations (Z) away from the mean by:
For example: Invoices at a particular depot have amounts that follow a normal distribution with a mean of £103.60 and a standard deviation of £8.75. What percentage of invoices would you expect to be over £120.05? [See Note 6]
First, we sketch figure 1 and transform the raw data X = £120.05 into a Z score, by deducting the mean of £103.60 and dividing by the standard deviation of £8.75:
Z = (120.05 – 103.60 = 16.45)/8.75 = +1.88 (above the mean).
Then look up the upside proportion in table 1. For Z = +1.88 the upside proportion is 0.0301 (3.01%). This is the blue-shaded area in figure 1.
We can also use the same formula:
Z score =
to go in the other direction. In other words, given a Z score, we can calculate the related raw data point X.
For example:As before, invoices have amounts that follow a normal distribution with a mean of £103.60 and a standard deviation of £8.75. Above what invoice amount would you expect 95% of invoices to lie? [See Note 7]
This requires two steps: work out the Z score of -1.6449 from the proportion above 95%; and calculate the data point X.
Sketch another planning diagram, this time like figure 4. We need a Z score that will give us a pink area above it of 95%. Look at the diagram. The Z score we need is the one at the left end of the 95% pink area. This is -Z (ie negative, not positive). Many students came unstuck at this point in the ESA exam, which the examiner highlighted (see A Common Mistake, below). Here, as elsewhere, drawing a diagram makes it clear and easy.
Finishing the question off, because of the symmetry and the total area adding up to 100%, we need the positive Z score where the blue area is 5%.
Z = 1.6449 in this case.
So the -Z figure we need is -1.6449.
Using:
Z score =
-1.6449 =
Rearranging this equation:
-1.6649 x 8.75 = X – 103.60
+103.60 – (1.6449 x 8.75) = X
= £89.21
Full marks, many congratulations! Now practise.
“This question had the lowest number of passes in the paper.
“The main issue came where students were required to take a Z-reading from the normal distribution table. Students were required to find the point where 95% of data lies above Z (-1.6449), but most attempts instead used +1.6449, giving an incorrect answer. This mistake was very common.”
Examiner’s Report, Economics and Statistical Analysis (ESA), October 2012
Note 1: Alternative versions of the normal table may give instead, for example, the proportions below Z (shaded green in figure 2).
Note 2: 0.9452 (94.52%) = 1 – 0.0548.
Note 3: 0.0301 (3.01%) being the same as the blue proportion above Z = 1.88, from Table 1.
Note 4: 0.9887 (98.87%) = 1 – 0.0113.
Note 5: This is on the ESA exam formula sheet.
Note 6: ESA exam Oct 2012, Q7(a).
Note 7: ESA exam Oct 2012, Q7(c).
Download the previous articles from this series and other useful study information from the exam tips area of the ACT student site at study.treasurers.org/examtips
Doug Williamson FCT is an examiner, tutor and exam scrutineer for six ACT exam courses
