
A recent Corporate Finance and Funding exam (April 2013, Q1) describes how a company chairman agreed to pay £400m for an acquisition, justified by an over-simplistic, multiple-based valuation. Among other requirements, we are asked to recalculate the value of the target using fundamental discounted cash flow (DCF) techniques. Our theoretically superior DCF valuation gives a much lower value than the purchase price of £400m agreed by the chairman. This acquisition is about to lose a lot of money.
Two frequent errors in DCF valuations are: not recognising that decline is negative growth; and not adjusting real terms figures, to add back inflation.
We know that the faster any future cash flows grow, the greater their total present value.
When cash flows are in stable growth (or decline) they can be valued as a simple perpetuity, using the formula:
Time 0 value = Time 1 cash flow ÷ (r – g).
Where r is the appropriate discount rate and g is the stable rate of growth (or decline).
For example, let’s assume the Time 1 cash flow is £10m and the discount rate (r) is 10% = 0.10.
When the rate of growth (g) is 2%, the term (r – g) is 0.10 – 0.02 = 0.08. The total value of the cash flows is £10m ÷ (r – g) = £10m ÷ 0.08 = £125m.
As the rate of growth (g) increases, the total value also increases as follows:
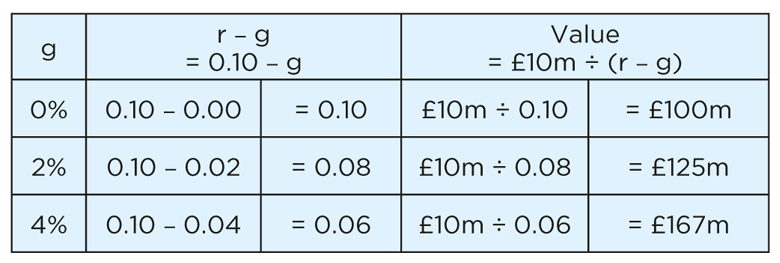
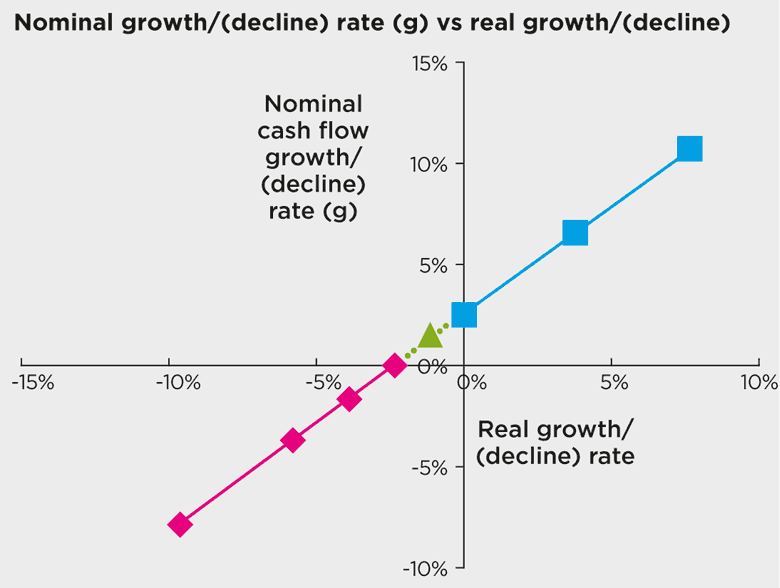
The total values for positive rates of growth are summarised in the blue part of the graph below. The greater the rate of growth, the greater the valuation.
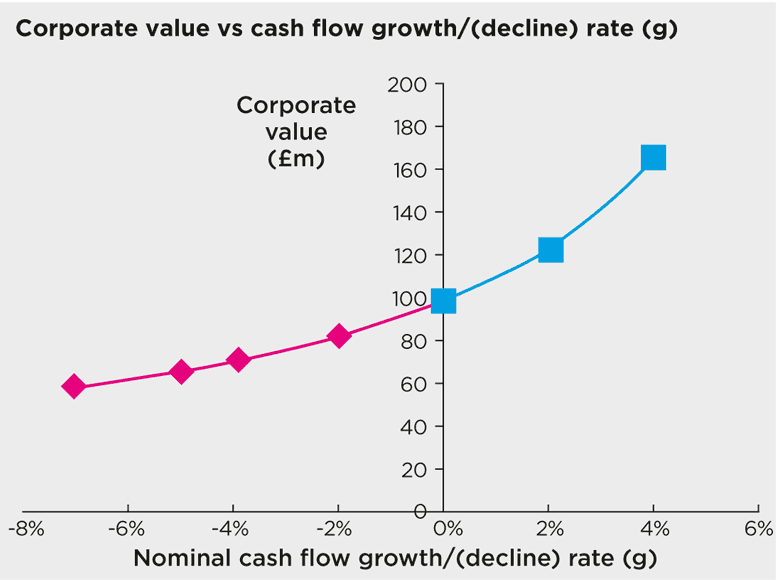
When growth rates fall and become negative, value is destroyed. This reduction in value is shown in the pink part of the graph above.
The valuation is still calculated by exactly the same perpetuity formula:
Time 0 value = Time 1 cash flow ÷ (r – g).
g is the stable rate of growth, or decline, just as before.
But now, when the cash flows are declining, the rate of growth (g) is a negative number.
For example, say the Time 1 cash flow is still £10m and the discount rate (r) is still 10% = 0.10.
When the rate of decline is 2%, g = -2%, and the term (r – g) becomes:
0.10 – (-0.02) = 0.10 + 0.02 = 0.12.
(Not 0.08.)
The total value of the cash flows now falls accordingly to: £10m ÷ 0.12 = £83m.
This is the first common error (a) highlighted by the examiner [see Growing Pains, below]. Minus minus calculations give a plus, not another minus. Many exam candidates miscalculated, getting the signs of their g terms the wrong way round, leading to overvaluations. These candidates risked losing their companies a lot of money in overpaying for (overvalued) acquisitions.
As the rate of decline worsens, the valuations decrease even further, as we see below:
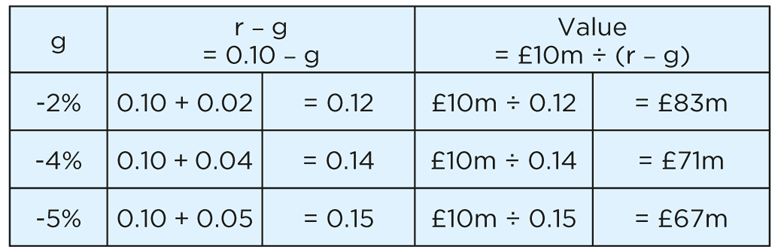
It’s your turn now. Calculate the total value of the cash flows when the rate of decline is 7%. Be careful to get your signs the right way round. The answer is at the end. [See Note 1 below]
The exam DCF valuation we saw earlier required handling the following calculation as part of its detailed workings:
Declining cash flow = £32.9m; discount rate = 9%; rate of decline = 1.6%.
Calculate the total value of these cash flows. [See Note 2 below]
Paying £400m for a business that is only worth £310m will lose £90m.
All of the amounts we’ve seen so far have been in normal cash terms (sometimes known as ‘nominal’ terms). By contrast, any ‘real’ amounts have been adjusted downwards to exclude inflation.
So when exam questions give rates of growth or decline ‘in real terms’, we need to adjust the given ‘real’ figures back into cash terms, by adding back the rate of inflation.
The necessary adjustment to a real rate of growth (or decline) is:
Nominal growth rate (g) = ( (1 + real growth rate) x (1 + inflation rate) ) – 1.
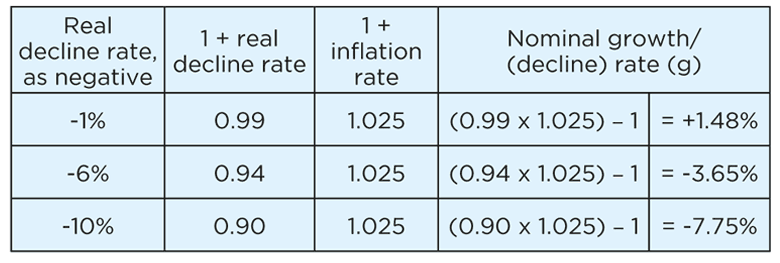
For example, when inflation is 2.5% = 0.025, nominal cash flow growth is:
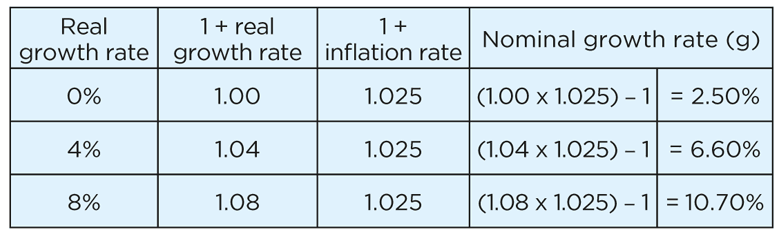
Notice in each case the nominal growth rate is roughly equal to the real growth rate plus the inflation of 2.5%. (For example, in the second row of the table, 4% + 2.5% = 6.5%, roughly 6.60%.)
Real rates of growth can also be negative. In this case, the resulting nominal growth rate may be negative or it may be positive, depending on the size of the expected inflation rate.
The related nominal growth rates (g) are the pink and green parts of the graph below.
The required adjustment is still:
Nominal growth rate (g) = ( (1 + real growth rate) x (1 + inflation rate) ) – 1.
The only difference is that now the real growth rate is a negative number.
For example, a 1% real rate of decline is -1% = -0.01, and (1 + real rate) = 1 + (-0.01) = 0.99, and so forth.
Forgetting to do this was the second error (b) noted by the examiner [see Growing Pains, below]. Practise it now. Calculate the nominal rate of growth or decline, when the real rate of decline is 4%. Inflation is 2.5%, as before. [See Note 3 below]
Keep practising this important technique to pick up easy exam marks. Best wishes for your successful studies and exam.
Note 1: g = -0.07. r – g = 0.10 + 0.07 = 0.17. VALUE = £10M ÷ 0.17 = £59M.
Note 2: g = -0.016. r – g = 0.09 + 0.016 = 0.106. VALUE = £32.9M ÷ 0.106 = £310M.
Note 3: (1 + REAL RATE) = 1 – 0.04 = 0.96. NOMINAL RATE = (0.96 x 1.025) – 1 = -1.6%.
“The compulsory question required the valuation of a potential acquisition. The most common errors related to the growth rate of the cash flows. Candidates either (a) did not realise that a negative growth rate has to be added to the discount rate, or (b) did not adjust the real negative growth rate for inflation.”
Examiner’s Report, Corporate Finance and Funding, April 2013
9% – (-1.6%) = 9% + 1.6% = 10.6%.
(Not 7.4%.)
A real rate is one that has been restated to exclude inflation. Real rates of growth and decline often need uplifting to add back inflation.
Download the previous articles from this series and other useful study information from the exam tips area of the ACT student site at study.treasurers.org/examtips
Doug Williamson FCT is an examiner, tutor and exam scrutineer for six ACT exam courses
