
Many financial situations involve exchanging money now and re-exchanging a (larger) fixed sum of money later.
Examples include: short-term fixed rate investment; short-term fixed rate borrowing; and discounting short-term financial instruments. The concept of exchanging and re-exchanging is identical in all three cases, and it isn’t too hard. But quoting conventions differ, often causing confusion. Drawing a timeline – and putting cash flows on it – will usually sort them out nicely.
Start by drawing a timeline and putting cash flows on it. This clarifies thinking
We’ll start with a simple investment and its cash flows. Then we’ll see the different ways in which the same cash flows are quoted in different financial markets.
Let’s say we’re considering a simple investment to pay out 10.0m (in a given currency) today, and get back 10.3m (in the same currency) in 180 days’ time. Is this a good deal?
Let’s start by drawing a timeline and putting the known cash flows onto it.
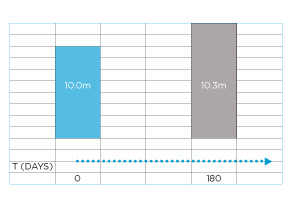
Clearly, we’re making a gain of 10.3m (the terminal value) less 10.0m (the initial amount) = 0.3m.
Expressed as a proportion of the initial amount of 10.0m, the gain of 0.3m is 0.3/10.0 = 3.000% per 180 days. (This is a yield basis of expressing our expected gain – see note 1.)
Expressed as a proportion of the terminal value 10.3m, the gain of 0.3m is 0.3/10.3 = 2.913% per 180 days. (This is a discount basis of expressing exactly the same cash flows and gain – see note 2.)
Note that it makes no difference at all to any of the cash flows, whether the gain of 0.3m is expressed (or described) as a yield or as a discount. We still pay out exactly the same 10.0m at the start, and we still get back exactly the same 10.3m at the end.
Well, that might be a good deal or it might not. It depends on what rate of return we could get from other comparable investments. We’ve already made a great start for our comparisons by calculating both the yield per 180 days and the discount percentage per 180 days, above.
But these figures are more conventionally quoted on a simple, annualised basis. We’ll do that next.
The simple nominal annual yield on a short-term investment is: (gain ÷ initial amount) x (conventional year ÷ days).
So in the case of our 10.0m initial amount returning 10.3m after 180 days, the nominal annual yield = (0.3 ÷ 10.0) x (conventional year ÷ 180).
The conventional year for GBP is 365 days.
So, if we’re considering a GBP 10.0m investment (paying back GBP 10.3m after 180 days), the simple nominal annual yield calculation is: (0.3/10.0) x (365/180) = 6.08%.
But the conventional calculation year for short-term USD and EUR is 360 days (not 365).
So if we had a USD 10.0m investment (paying back USD 10.3m after the same 180 days), the nominal annual yield calculation would be a lower figure based on 360 days: (0.3/10.0) x (360/180) = 6.00%.
The 360 days basis of calculation is sometimes known as ‘act/360’, meaning ‘actual’ days over 360 days.
The second important question for the exam is: ‘Yield or discount rate?’ We’ll look at that next.
Short-term discount rates are based on terminal values (rather than on initial amounts).
The annual discount rate on a short-term investment is: (gain/terminal value) x (conventional year/days).
In the same case of our 10.0m investment returning 10.3m terminal value after 180 days, the annual discount rate = (0.3/10.3) x (conventional year/180).
We saw that the conventional year for GBP is 365 days.
So for a GBP 10.0m investment (paying back GBP 10.3m after 180 days), the calculation is: (0.3/10.3) x (365/180) = 5.91%.
But it’s different for USD and EUR. Again, the conventional calculation year for short-term USD and EUR is 360 days (not 365).
So if we had a USD 10.0m investment (paying back USD 10.3m after the same 180 days), the annual discount rate calculation would again be lower: (0.3/10.3) x (360/180) = 5.83%.
Three questions in a recent International Treasury Management (ITM) exam tested these calculations.
What is the holding period yield (act/360 basis) for a USD certificate of deposit with a face value of 9.9m bought for 10.0m and sold 200 days later at 10.3m?
The relevant cash flows for the investor are the investment of USD 10.0m and the sale proceeds of USD 10.3m. Drawing a timeline clarifies this and helps to avoid the red herring (irrelevant) USD 9.9m, which is not a cash flow.
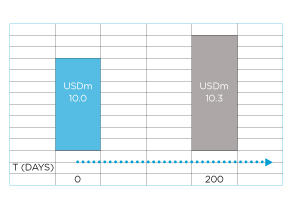
How many days per year? The investment is in USD, so we’d expect 360 days. And this question also (very helpfully) confirms the ‘act/360’ basis.
Yield or discount rate? This question expressly asks for a yield. So we’ll use an annual yield calculation (based on the gain of USD 0.3m and the USD 10.0m initial amount) on a 360-day basis over 200 days: 0.3/10.0 x 360/200 = 5.40%.
The next calculations in the same ITM exam contained a discount rate as well as a yield.
A firm issues 91-day zero coupon commercial paper with a face value of USD 50.0m and receives issue proceeds of USD 49.4m. What rates would this instrument be quoted at in the USCP market and in the ECP market?
With no issue costs, the investor’s return and the issuer’s borrowing cost are the same.
So our calculation is based simply on the USD 50.0m and the USD 49.4m. The gain is 50.0m – 49.4m = 0.6m.
How many days per year? The investment is in USD, so 360 days.
Yield or discount rate? USCP is US commercial paper, which is quoted on a discount basis. So the relevant 360-day discount rate calculation (based on the terminal value of USD 50.0m) is: (0.6/50.0) x (360/91) = 4.75% for the USCP market.
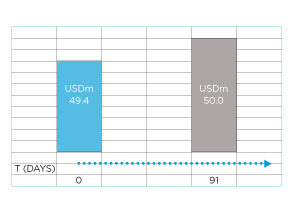
ECP is euro commercial paper, which is quoted on a yield basis. So the relevant 360-day yield calculation (based on the initial amount of USD 49.4m) is: (0.6/49.4) x (360/91) = 4.80% for the ECP market.
Finally, here’s a harder question from the same ITM exam.
A customer is due to pay GBP 1m, 60 days after the invoice date. You offer a 1.5% discount for settlement 28 days after the invoice date. Calculate the cost of discount as a yield (act/365 basis).
We can use exactly the same timeline structure of terminal value, initial amount and a difference. The terminal value is GBP 1m. The 1.5% discount is a flat amount on the GBP 1m, not per annum. So the money discount is simply 0.015 x GBP 1m = GBP 0.015m. And the initial amount is 1 – 0.015 = GBP 0.985m.
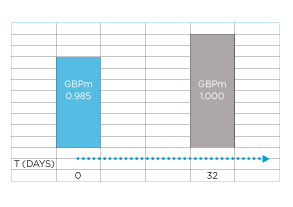
This is a yield calculation on a 365 days basis.
The borrowing cost is GBP 0.015m, the initial amount is GBP 0.985m, and the time difference is 60 – 28 days = 32 days.
So the required yield figure is 0.015/0.985 x 365/32 = 17.4%.
This is very expensive. Far more expensive than you might expect based on the headline number of 1.5%. In the exam as in life.
To quote your examiners:
“The average pass rate for questions testing calculations, at 54%, was significantly lower than for those testing knowledge, at 80%. Candidates are recommended to pay particular attention to this area in the future... start by drawing a timeline and putting cash flows on it. This clarifies thinking.”
Download the previous articles from this series and other useful study information from the exam tips area of the ACT student site at study.treasurers.org/examtips
Doug Williamson FCT is an examiner, tutor and exam scrutineer for six ACT exam courses
